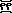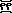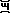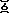)3
)3
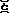 )2
)2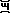
 )1
)1
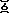 )0
)0 ) + (3 * {
) + (3 * { })
})
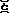 ) + (2 * {
) + (2 * { })
})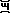
 ) + (1 * {
) + (1 * { })
})
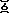 ) + (0 * {
) + (0 * { })
}) 's we need.
's we need. ) + (
) + ( +
+ +
+ )
)
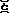 ) + (
) + ( +
+ )
)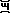
 ) + (
) + ( )
)
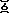 ) + (0)
) + (0) ) + (
) + ( +
+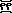 )
)
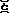 ) + (
) + (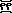 )
)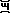
 ) + (
) + ( )
)
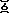 ) + (0)
) + (0)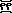 =
=  +
+


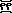

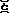
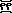
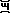



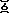


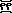

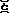
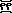
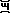



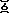
Note! Except for when we use subscript ``0'' (the far right side) there is a rule that 1's in the 1's place are absorbed by an
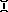 ,
,  ,
or
,
or 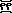 on the right. So if we
changed the ``5'' in [65]2 to a ``1'' in the above; the reduction would go:
as
on the right. So if we
changed the ``5'' in [65]2 to a ``1'' in the above; the reduction would go:
as ) + (
) + ( +
+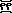 )
)
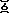 ) + (
) + (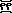 )
)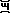
 ) + (
) + ( )
)
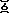 ) + (0)
) + (0)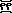 =
=  +
+